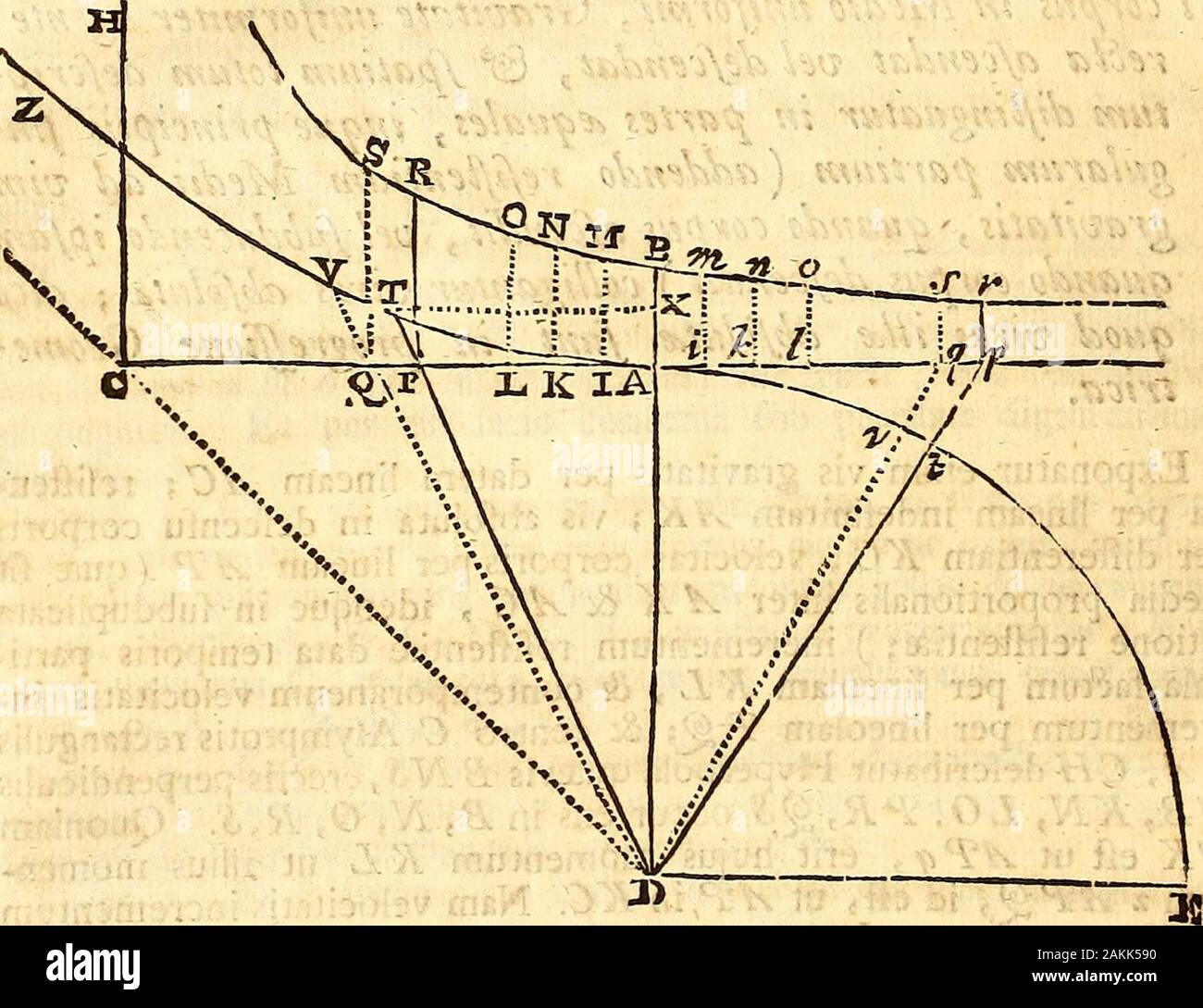
Philosophiae naturalis principia mathematica . amp;^et rec-tangulum KLXKN ut ATxKCxKN, hoc eft, ob dato rec-rangulum ^CXi^iV, ut a. Aree Atqui Hyperbolicae KNOLad reftangulam KLxKNratio ultima , ubi coeunt punda K&Lyeft sequalitatis. Area Ergo illa Hyperbolica evanefcens elt ut AT.Compbnitur area igitur tota Hyperbolica ABOL ex particulisKNOL velocitati a femper proportionalibus , & proptereaIpatio velocitate ifta defcripto proportionalis eft, Dividatur jamarea illa in aequales partes ABMIy IMNK, KNOL, &c. & Vi- ¥fz res za8 PHILOSOPHIiE NATURALIS DxMoTu res abfolutae AC, IC, KC, LC, &c. er

• Collaboratore: The Reading Room
• ID dell’immagine: 2AKK590
• Dimensioni dei file: 7,1 MB (357,1 KB Download compresso)
• Liberatorie: Modello - no | Proprietà - no
• Dimensioni: 1802 x 1386 px | 30,5 x 23,5 cm | 12 x 9,2 inches | 150dpi

Altre informazioni

Questa foto è un'immagine di pubblico dominio, il che significa che il copyright è scaduto o che il titolare del copyright ha rinunciato a tale diritto. Alamy addebita un costo per l'accesso alla copia ad alta risoluzione dell'immagine.

Questa immagine potrebbe avere delle imperfezioni perché è storica o di reportage.

Philosophiae naturalis principia mathematica . amp;^et rec-tangulum KLXKN ut ATxKCxKN, hoc eft, ob datum rec-rangulum ^CXi^iV, ut AT. Atqui areas Hyperbolicae KNOLad reftangulam KLxKNratio ultima , ubi coeunt punda K&Lyeft sequalitatis. Ergo area illa Hyperbolica evanefcens elt ut AT.Compbnitur igitur area tota Hyperbolica ABOL ex particulisKNOL velocitati AT femper proportionalibus , & proptereaIpatio velocitate ifta defcripto proportionalis eft, Dividatur jamarea illa in partes aequales ABMIy IMNK, KNOL, &c. & vi- ¥fz res za8 PHILOSOPHIiE NATURALIS DxMoTu res abfolutae AC, IC, KC, LC, &c. erunt in progrefficme Geo-Co&poRUM, nietrica. ^E.T). Et fimili argumento, in afcenfu corporis, fu-mendo , ad contrariam partem punfti A, aequales areas ABmi, imnky knol, &c. conftabit quod vires abfolutae AC, iC, kC, lC, &c. funt continue proportionales. Ideoque fi fpatia omnia in afcen-fu & defcenfu capiantur aequalia; omnes vires abfolutae /C, kC, iC, AC) ICy KC, LC, &c. erunt coniinue proportionales. ^E.D.. Corol. I. Hinc fi fpatium defcriptum exponatur per aream Hy-perbolicam ABNK; exponi poflunt vis gravitatis, velocitas cor-poris & refillentia Medii per lineas AC, AT 8c ^^refpeftive ;& vice verfa. Corol. z. Et velocifatismaxims, quam corpus in infinitum def-cendendo poteft unquam acquirere, exponens eft linea AC. Corol. 3. Igitur ft in data aliqua velocitate cognofcatur refiften-tia Medii, invenietur velocitas maxima, fumendo ipfam ad veloci- latem PRINCIPIA MATHEMATICA. zic> .tatem iilam datam iti fubduplicata ratiohe, quam habet vis Gravi-tatis ad Medii refiftentiam illam cognitam. .;. j;:^;/;/ • pROPOsiTio IX. theoremAvil Poftthjam demonftrath , dico qmdfi Tangentes angulorumfeB:oris Ctrcularh ^ feBorh H^yperbolki fumantur velo^cttattbus proportionales , exiftente radio jufta magnitudinis : erit tempus omne afcenfus futuri ut feBor Circuli, ^ tempus omne defcenftds prneteriti ut feBor Hyperbola. Reftae AC, qua vis gravitatis exponitur , perpendicularis & ge-qualis d

Parole chiave associate all'immagine

• booksubj
• booksubjectmechanics